English
Zadanie Permutacje (prm)
Permutations
Memory limit: 32 MB
A permutation1
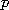of a set 
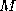is called an involution if 
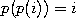for each 
.
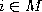By a bracket expression of length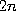 
we mean a word of length 
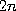consisting only of the characters '('
and ')'.
A bracket expression is called correct if the number of opening brackets in the expression equals the
number of closing brackets and in every prefix of the expression the number
of the characters '(' is no less than the number of characters ')'.
We say that a permutation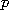 
of length 
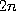encodes a bracket expression of length 
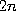, if
opening brackets of the expression (from left to right) are located at positions 
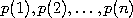, and closing
brackets - also from left to right - at positions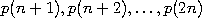 
.
In particular, in such a case both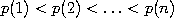 
and
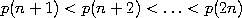hold.
The values of a permutation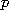 
for several arguments are known.
It should be determined in how many ways the remaining values of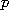 
can be determined in such a way that it is an involution and it encodes
a correct bracket expression.
Input
The first line of the standard input contains two integers
and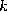 
(
, 
)
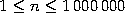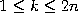separated by a single space.
Each of the following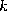 
lines contains one pair of space-separated integers;
the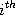 
of these lines contains numbers
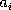and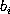 
(
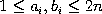), meaning that 
.
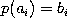All values 
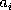are distinct and all values 
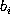are distinct.
Output
The first and only line of the standard output should contain a single integer:
the number of permutations of the set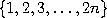 
that:
are involutions, encode some correct bracket expression, and for which
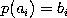holds for each 
.
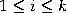Example
For the input data:
3 4 1 1 2 2 4 3 6 6
the correct result is:
1
Explanation of the example:
The only permutation that complies with requirements of the task is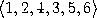 
,
and it encodes the following bracket expression: (()()).
1. A permutation of a set
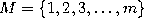is any one-to-one function 
.
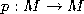Task author: Dariusz Leniowski.